Assembias_HOD_Quenching_Model¶

class halotools.halo_occupation.Assembias_HOD_Quenching_Model[source] [edit on github]¶

Bases: halotools.halo_occupation.Assembias_HOD_Model

Abstract base class for any HOD model in which both galaxy abundance and galaxy quenching on Mvir plus an additional property.

Methods Summary

`conformity_case_ratio_centrals`(...)	The bounds on the conformity function depend on the other HOD model parameters.
`conformity_case_ratio_satellites`(...)	The bounds on the conformity function depend on the other HOD model parameters.
`conformity_centrals`(primary_halo_property, ...)	Conformity function as pertains to centrals :Parameters: halo_type : array_like Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
`conformity_satellites`(primary_halo_property, ...)	Conformity function as pertains to satellites.
`maximum_conformity_centrals`(...)	The maximum allowed value of the conformity function, as pertains to centrals.
`maximum_conformity_satellites`(...)	The maximum allowed value of the conformity function, as pertains to satellites.
`mean_quenched_fraction_centrals`(...)	Override the baseline HOD method used to compute central quenched fraction.
`mean_quenched_fraction_satellites`(...)	Override the baseline HOD method used to compute satellite quenched fraction.
`minimum_conformity_centrals`(...)	The minimum allowed value of the inflection function, as pertains to centrals.
`minimum_conformity_satellites`(...)	The minimum allowed value of the inflection function, as pertains to satellites.
`unconstrained_central_conformity_halo_type1`(...)	Method determining $\tilde{\mathcal{C}}_{cen_{Q}}(p \| h_{1})$ , the unconstrained excess quenched fraction of centrals in halos of primary property $p$ and secondary property type $h_{1}$ .
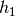`unconstrained_satellite_conformity_halo_type1`(...)	Method determining 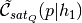$\tilde{\mathcal{C}}_{sat_{Q}}(p \| h_{1})$ , the unconstrained excess quenched fraction of satellites in halos of primary property $p$ and secondary property type $h_{1}$ .

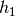Methods Documentation

conformity_case_ratio_centrals(primary_halo_property, halo_type)[source] [edit on github]¶

The bounds on the conformity function depend on the other HOD model parameters. This function determines which case should be used in computing the conformity bounds.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

conformity_case_ratio : array_like

Array giving the ratio that determines how maximum conformity is computed.

conformity_case_ratio_satellites(primary_halo_property, halo_type)[source] [edit on github]¶

The bounds on the conformity function depend on the other HOD model parameters. This function determines which case should be used in computing the conformity bounds.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

conformity_case_ratio : array_like

Array giving the ratio that determines how maximum conformity is computed.

conformity_centrals(primary_halo_property, halo_type)[source] [edit on github]¶

Conformity function as pertains to centrals

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_conformity : array_like

Array giving the multiple by which the mean quenched fraction is boosted.

conformity_satellites(primary_halo_property, halo_type)[source] [edit on github]¶

Conformity function as pertains to satellites.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_conformity : array_like

Array giving the multiple by which the mean quenched fraction is boosted.

maximum_conformity_centrals(primary_halo_property, halo_type)[source] [edit on github]¶

The maximum allowed value of the conformity function, as pertains to centrals.

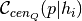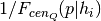The combinatorics of assembly-biased HODs are such that the conformity function $\mathcal{C}_{cen_{Q}}(p | h_{i})$ can exceed neither $1 / \mathcal{I}_{cen}(p | h_{i})P_{h_{i}}(p)$ , nor $1 / F_{cen_{Q}}(p | h_{i})$ .

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_maximum_conformity : array_like

Maximum allowed value of the conformity function, as pertains to centrals.

maximum_conformity_satellites(primary_halo_property, halo_type)[source] [edit on github]¶

The maximum allowed value of the conformity function, as pertains to satellites.

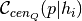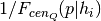The combinatorics of assembly-biased HODs are such that the conformity function $\mathcal{C}_{cen_{Q}}(p | h_{i})$ can exceed neither $1 / \mathcal{I}_{cen}(p | h_{i})P_{h_{i}}(p)$ , nor $1 / F_{cen_{Q}}(p | h_{i})$ .

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_maximum_conformity : array_like

Maximum allowed value of the conformity function, as pertains to satellites.

mean_quenched_fraction_centrals(primary_halo_property, halo_type)[source] [edit on github]¶

Override the baseline HOD method used to compute central quenched fraction.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

quenched_fraction : array_like

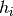$h_{i}$ -conditioned central quenched fraction as a function of the primary halo property $p$ .

$F_{Q}^{cen}(p | h_{i}) = \mathcal{C}_{cen}(p | h_{i})F_{Q}^{cen}(p)$

mean_quenched_fraction_satellites(primary_halo_property, halo_type)[source] [edit on github]¶

Override the baseline HOD method used to compute satellite quenched fraction.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

quenched_fraction : array_like

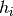$h_{i}$ -conditioned central quenched fraction as a function of the primary halo property $p$ .

$F_{Q}^{sat}(p | h_{i}) = \mathcal{C}_{sat}(p | h_{i})F_{Q}^{sat}(p)$

minimum_conformity_centrals(primary_halo_property, halo_type)[source] [edit on github]¶

The minimum allowed value of the inflection function, as pertains to centrals.

The combinatorics of assembly-biased HODs are such that the conformity function 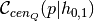$\mathcal{C}_{cen_{Q}}(p | h_{0,1})$ must exceed both a and b.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_minimum_conformity : array_like

Minimum allowed value of the conformity function, as pertains to centrals.

minimum_conformity_satellites(primary_halo_property, halo_type)[source] [edit on github]¶

The minimum allowed value of the inflection function, as pertains to satellites.

The combinatorics of assembly-biased HODs are such that the conformity function 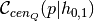$\mathcal{C}_{cen_{Q}}(p | h_{0,1})$ must exceed both a and b.

Parameters:

halo_type : array_like

Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.

primary_halo_property : array_like

Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.

Returns:

output_minimum_conformity : array_like

Minimum allowed value of the conformity function, as pertains to satellites.

unconstrained_central_conformity_halo_type1(primary_halo_property)[source] [edit on github]¶

Method determining $\tilde{\mathcal{C}}_{cen_{Q}}(p | h_{1})$ , the unconstrained excess quenched fraction of centrals in halos of primary property $p$ and secondary property type $h_{1}$ .

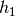Can be any arbitrary function, subject only to the requirement that it be bounded. Constraints on the value of this function required in order to keep the unconditioned quenched fraction 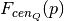$F_{cen_{Q}}(p)$ fixed are automatically applied by conformity_centrals.

Notes

If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for centrals.

unconstrained_satellite_conformity_halo_type1(primary_halo_property)[source] [edit on github]¶

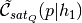Method determining $\tilde{\mathcal{C}}_{sat_{Q}}(p | h_{1})$ , the unconstrained excess quenched fraction of satellites in halos of primary property $p$ and secondary property type $h_{1}$ .

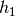Can be any arbitrary function, subject only to the requirement that it be bounded. Constraints on the value of this function required in order to keep the unconditioned quenched fraction 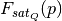$F_{sat_{Q}}(p)$ fixed are automatically applied by conformity_satellites.

Notes

If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for centrals.

Navigation

Assembias_HOD_Quenching_Model¶

Page Contents