Assembias_HOD_Model¶
- class halotools.halo_occupation.Assembias_HOD_Model[source] [edit on github]¶
Bases: halotools.halo_occupation.HOD_Model
Abstract base class for any HOD model with assembly bias.
In this class of models, central and/or satellite mean occupation depends on some primary property, such as
 , and the mean occupations are modulated by some secondary property,
such as
, and the mean occupations are modulated by some secondary property,
such as  .
.Notes
All implementations of assembly bias are formulated in such a way that the baseline occupation statistics are kept fixed. For example, suppose that a subclass of this class introduces a dependence of
 on the
secondary halo property
on the
secondary halo property  , and that the primary halo property is the traditional
, and that the primary halo property is the traditional
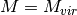 . Then in narrow bins of
. Then in narrow bins of 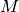 , host halos in the simulation
will be rank-ordered by
, host halos in the simulation
will be rank-ordered by  ,
and assigned a halo type
,
and assigned a halo type 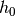 or
or 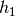 ,
where the halos may be split by any fraction into the two halo types,
and this fractional split may vary with
,
where the halos may be split by any fraction into the two halo types,
and this fractional split may vary with 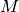 according to
any arbitrary function
according to
any arbitrary function  supplied by the model
via the halo_type1_fraction_centrals method.
The
supplied by the model
via the halo_type1_fraction_centrals method.
The  -dependence of central occupation is governed by
the central inflection function
-dependence of central occupation is governed by
the central inflection function  via
via
 .
The subclass implementing assembly bias need only supply any arbitrary function
.
The subclass implementing assembly bias need only supply any arbitrary function
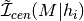 via the unconstrained_central_inflection_halo_type1
method, and a variety of the built-in methods of this class will automatically apply appropriate boundary
conditions to determine
via the unconstrained_central_inflection_halo_type1
method, and a variety of the built-in methods of this class will automatically apply appropriate boundary
conditions to determine  from
from 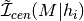 ,
such that the following constraint is satisfied:
,
such that the following constraint is satisfied: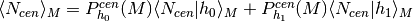 .
.Therefore, assembly bias of arbitrary strength can be introduced in a way that preserves the baseline occupation statistics, allowing users of halotools to isolate the pure influence of assembly bias on any observational statistic that can be computed in a mock.
There are entirely independent functions governing satellite galaxy assembly bias, allowing the role of centrals and satellites to be parsed. The secondary property used to modulate the occupation statistics of centrals can be distinct from the property modulating satellite occupation.
The secondary halo property can be any halo property computable from a halo catalog and/or merger tree. The user need only change secondary_halo_property_centrals_key and/or secondary_halo_property_satellites_key to create identical assembly-biased models based on different secondary properties. Likewise, the primary halo property may also be varied by changing primary_halo_property_key, provided that the user supplies a baseline HOD model predicated upon the suppiled primary halo property. Thus this class allows one to create mock universes possessing assembly bias of arbitrary strength and character, subject to the caveat that the occupation statistics can be parameterized by two halo properties.
Finally, the secondary property modulating the assembly bias need not be a physical attribute of the host halo. For example, the Satcen_Correlation_Polynomial_HOD_Model subclass can be used to create mocks in which of satellite occupation statistics are modulated by whether or not there is a central galaxy residing in the host halo.
Attributes Summary
baseline_hod_model Underlying HOD model, about which assembly bias modulates galaxy abundance and intra-halo spatial distribution. primary_halo_property_key String providing halo catalog dictionary key pointing to primary halo property. secondary_halo_property_centrals_key String providing halo catalog dictionary key pointing to primary halo property. secondary_halo_property_satellites_key String providing halo catalog dictionary key pointing to primary halo property. Methods Summary
halo_type1_fraction_centrals(...) Determines  , the fractional representation of host halos of type
, the fractional representation of host halos of type 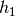 as a function of the primary halo property
as a function of the primary halo property  , as pertains to centrals.
, as pertains to centrals.halo_type1_fraction_satellites(...) Determines  , the fractional representation of host halos of type
, the fractional representation of host halos of type 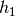 as a function of the primary halo property
as a function of the primary halo property  , as pertains to satellites.
, as pertains to satellites.halo_type_calculator(primary_halo_property, ...) Determines the assembly bias type of the input halos, as pertains to centrals. halo_type_fraction_centrals(...) Using the function halo_type1_fraction_centrals required by concrete subclasses, this method determines  , the fractional representation of host halos of input halo type
, the fractional representation of host halos of input halo type 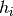 as a function of input primary halo property
as a function of input primary halo property  , as pertains to centrals.
, as pertains to centrals.halo_type_fraction_satellites(...) Using the function halo_type1_fraction_satellites required by concrete subclasses, this method determines 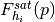 , the fractional representation of host halos of input halo type
, the fractional representation of host halos of input halo type 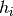 as a function of input primary halo property
as a function of input primary halo property  , as pertains to satellites.
, as pertains to satellites.inflection_centrals(primary_halo_property, ...) Method determining 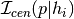 , the true excess probability that halos of primary property
, the true excess probability that halos of primary property  and secondary property type
and secondary property type 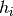 host a central galaxy.
host a central galaxy.inflection_satellites(primary_halo_property, ...) Method determining  , the true excess probability that halos of primary property
, the true excess probability that halos of primary property  and secondary property type
and secondary property type 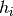 host a satellite galaxy.
host a satellite galaxy.maximum_inflection_centrals(...) The maximum allowed value of the inflection function, as pertains to centrals. maximum_inflection_satellites(...) Maximum allowed value of the inflection function, as pertains to satellites. mean_ncen(primary_halo_property, halo_type) Override the baseline HOD method used to compute mean central occupation. mean_nsat(primary_halo_property, halo_type) Override the baseline HOD method used to compute mean satellite occupation. minimum_inflection_centrals(...) The minimum allowed value of the inflection function, as pertains to centrals. unconstrained_central_inflection_halo_type1(...) Method determining 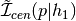 , the unconstrained excess probability that halos of primary property
, the unconstrained excess probability that halos of primary property  and secondary property type
and secondary property type 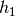 host a central galaxy.
host a central galaxy.unconstrained_satellite_inflection_halo_type1(...) Method determining  , the unconstrained excess probability that halos of primary property
, the unconstrained excess probability that halos of primary property  and secondary property type
and secondary property type 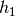 host a satellite galaxy.
host a satellite galaxy.Attributes Documentation
- baseline_hod_model¶
Underlying HOD model, about which assembly bias modulates galaxy abundance and intra-halo spatial distribution. Must be one of the supported subclasses of HOD_Model. The baseline HOD model can in principle be driven by any host halo property.
- primary_halo_property_key¶
String providing halo catalog dictionary key pointing to primary halo property. Necessary to ensure self-consistency between underlying halo model, occupation-dependence of assembly bias, and color-dependence of assembly bias.
- secondary_halo_property_centrals_key¶
String providing halo catalog dictionary key pointing to primary halo property. Necessary to ensure self-consistency between underlying halo model, occupation-dependence of assembly bias, and color-dependence of assembly bias.
- secondary_halo_property_satellites_key¶
String providing halo catalog dictionary key pointing to primary halo property. Necessary to ensure self-consistency between underlying halo model, occupation-dependence of assembly bias, and color-dependence of assembly bias.
Methods Documentation
- halo_type1_fraction_centrals(primary_halo_property)[source] [edit on github]¶
Determines
 ,
the fractional representation of host halos of type
,
the fractional representation of host halos of type 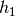 as a function of the primary halo property
as a function of the primary halo property  , as pertains to centrals.
, as pertains to centrals.Notes
If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for centrals, regardless of the behavior of unconstrained_central_inflection_halo_type1.
Code currently assumes that this function has already been guaranteed to be bounded by zero and unity. This will need to be fixed to be more defensive, so that any bounded function will automatically be converted to a proper PDF.
- halo_type1_fraction_satellites(primary_halo_property)[source] [edit on github]¶
Determines
 ,
the fractional representation of host halos of type
,
the fractional representation of host halos of type 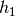 as a function of the primary halo property
as a function of the primary halo property  , as pertains to satellites.
, as pertains to satellites.Notes
If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for satellites, regardless of the behavior of unconstrained_satellite_inflection_halo_type1.
Code currently assumes that this function has already been guaranteed to be bounded by zero and unity. This will need to be fixed to be more defensive, so that any bounded function will automatically be converted to a proper PDF.
- halo_type_calculator(primary_halo_property, secondary_halo_property, halo_type_fraction_function, bin_spacing=0.1)[source] [edit on github]¶
Determines the assembly bias type of the input halos, as pertains to centrals.
Method bins the input halos by the primary halo property
 , splits each bin
according to the value of halo_type_fraction_centrals in the bin,
and assigns halo type
, splits each bin
according to the value of halo_type_fraction_centrals in the bin,
and assigns halo type 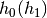 to the halos below (above) the split.
to the halos below (above) the split.Parameters: primary_halo_property : array_like
Array with elements equal to the primary_halo_property
secondary_halo_property : array_like
Array with elements equal to the value of the secondary_halo_property
Returns: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
- halo_type_fraction_centrals(primary_halo_property, halo_type)[source] [edit on github]¶
Using the function halo_type1_fraction_centrals required by concrete subclasses, this method determines
 , the fractional representation
of host halos of input halo type
, the fractional representation
of host halos of input halo type 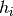 as a function of input primary halo property
as a function of input primary halo property  , as pertains to centrals.
, as pertains to centrals.Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: output_halo_type_fraction : array_like
Each element gives the probability that a halo with input primary halo property
 has input halo type
has input halo type 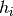
- halo_type_fraction_satellites(primary_halo_property, halo_type)[source] [edit on github]¶
Using the function halo_type1_fraction_satellites required by concrete subclasses, this method determines
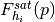 , the fractional representation
of host halos of input halo type
, the fractional representation
of host halos of input halo type 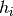 as a function of input primary halo property
as a function of input primary halo property  , as pertains to satellites.
, as pertains to satellites.Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: output_halo_type_fraction : array_like
Each element gives the probability that a halo with input primary halo property
 has input halo type
has input halo type 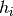
- inflection_centrals(primary_halo_property, halo_type)[source] [edit on github]¶
Method determining
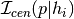 ,
the true excess probability that halos of primary property
,
the true excess probability that halos of primary property  and
secondary property type
and
secondary property type 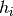 host a central galaxy.
host a central galaxy.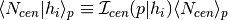 .
.All of the behavior of this function derives from unconstrained_central_inflection_halo_type1 and halo_type1_fraction_centrals, both of which are required methods of the concrete subclass. The function
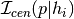 only differs from
only differs from 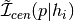 in regions of HOD parameter space where the provided values of
in regions of HOD parameter space where the provided values of
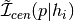 would violate the following constraint:
would violate the following constraint: where the RHS is given by baseline_hod_model.
where the RHS is given by baseline_hod_model.Defining
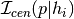 in this way
guarantees that the parameters modulating assembly bias have zero intrinsic covariance with parameters governing
the traditional HOD. Therefore, any degeneracy between the assembly bias parameters
and the traditional HOD parameters in the posterior likelihood is purely due to degenerate effects
of the parameters on the chosen observable.
in this way
guarantees that the parameters modulating assembly bias have zero intrinsic covariance with parameters governing
the traditional HOD. Therefore, any degeneracy between the assembly bias parameters
and the traditional HOD parameters in the posterior likelihood is purely due to degenerate effects
of the parameters on the chosen observable.
- inflection_satellites(primary_halo_property, halo_type)[source] [edit on github]¶
Method determining
 ,
the true excess probability that halos of primary property
,
the true excess probability that halos of primary property  and
secondary property type
and
secondary property type 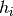 host a satellite galaxy.
host a satellite galaxy.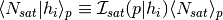 .
.All of the behavior of this function derives from unconstrained_satellite_inflection_halo_type1 and halo_type1_fraction_satellites, both of which are required methods of the concrete subclass. The function
 only differs from
only differs from  in regions of HOD parameter space where the provided values of
in regions of HOD parameter space where the provided values of
 would violate the following constraint:
would violate the following constraint: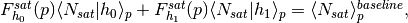 where the RHS is given by baseline_hod_model.
where the RHS is given by baseline_hod_model.Defining
 in this way
guarantees that the parameters modulating assembly bias have zero intrinsic covariance with parameters governing
the traditional HOD. Therefore, any degeneracy between the assembly bias parameters
and the traditional HOD parameters in the posterior likelihood is purely due to degenerate effects
of the parameters on the chosen observable.
in this way
guarantees that the parameters modulating assembly bias have zero intrinsic covariance with parameters governing
the traditional HOD. Therefore, any degeneracy between the assembly bias parameters
and the traditional HOD parameters in the posterior likelihood is purely due to degenerate effects
of the parameters on the chosen observable.
- maximum_inflection_centrals(primary_halo_property, halo_type)[source] [edit on github]¶
The maximum allowed value of the inflection function, as pertains to centrals.
The combinatorics of assembly-biased HODs are such that the inflection function
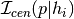 can exceed neither
can exceed neither
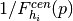 , nor
, nor 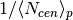 .
The first condition is necessary to keep fixed
the unconditioned mean central occupation
.
The first condition is necessary to keep fixed
the unconditioned mean central occupation  ;
the second condition is necessary to ensure that
;
the second condition is necessary to ensure that
 .
.Additionally,
 ,
which is applied not by this function but within inflection_centrals.
,
which is applied not by this function but within inflection_centrals.Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: output_maximum_inflection : array_like
Maximum allowed value of the inflection function, as pertains to centrals.
- maximum_inflection_satellites(primary_halo_property, halo_type)[source] [edit on github]¶
Maximum allowed value of the inflection function, as pertains to satellites.
The combinatorics of assembly-biased HODs are such that the inflection function
 can exceed
can exceed
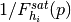 , or it would be impossible to keep fixed
the unconditioned mean satellite occupation
, or it would be impossible to keep fixed
the unconditioned mean satellite occupation  .
.Additionally,
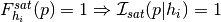 ,
which is applied not by this function but within inflection_satellites.
,
which is applied not by this function but within inflection_satellites.Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: output_maximum_inflection : array_like
Maximum allowed value of the inflection function, as pertains to satellites.
- mean_ncen(primary_halo_property, halo_type)[source] [edit on github]¶
Override the baseline HOD method used to compute mean central occupation.
Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: mean_ncen : array_like
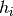 -conditioned mean central occupation as a function of the primary halo property
-conditioned mean central occupation as a function of the primary halo property  .
.
- mean_nsat(primary_halo_property, halo_type)[source] [edit on github]¶
Override the baseline HOD method used to compute mean satellite occupation.
Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: mean_nsat : array_like
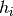 -conditioned mean satellite occupation as a function of the primary halo property
-conditioned mean satellite occupation as a function of the primary halo property  .
.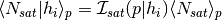
- minimum_inflection_centrals(primary_halo_property, halo_type)[source] [edit on github]¶
The minimum allowed value of the inflection function, as pertains to centrals.
The combinatorics of assembly-biased HODs are such that the inflection function
 can neither be negative
(which would be uphysical) nor fall below
can neither be negative
(which would be uphysical) nor fall below

Parameters: halo_type : array_like
Array with elements equal to 0 or 1, specifying the type of the halo whose fractional representation is being returned.
primary_halo_property : array_like
Array with elements equal to the primary_halo_property at which the fractional representation of the halos of input halo_type is being returned.
Returns: output_maximum_inflection : array_like
Maximum allowed value of the inflection function, as pertains to centrals.
- unconstrained_central_inflection_halo_type1(primary_halo_property)[source] [edit on github]¶
Method determining
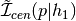 ,
the unconstrained excess probability that halos of primary property
,
the unconstrained excess probability that halos of primary property  and
secondary property type
and
secondary property type 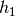 host a central galaxy.
host a central galaxy.Can be any arbitrary function, subject only to the requirement that it be bounded. Constraints on the value of this function required in order to keep the baseline
 fixed
are automatically applied by inflection_centrals.
fixed
are automatically applied by inflection_centrals.Notes
If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for centrals.
- unconstrained_satellite_inflection_halo_type1(primary_halo_property)[source] [edit on github]¶
Method determining
 ,
the unconstrained excess probability that halos of primary property
,
the unconstrained excess probability that halos of primary property  and
secondary property type
and
secondary property type 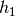 host a satellite galaxy.
host a satellite galaxy.Can be any arbitrary function, subject only to the requirement that it be bounded. Constraints on the value of this function required in order to keep the baseline
 fixed
are automatically applied by inflection_satellites.
fixed
are automatically applied by inflection_satellites.Notes
If this function is set to be either identically unity or identically zero, there will be no assembly bias effects for satellites.