The bottom-left panel of the Binary Maker output shows the radial velocity curve of the binary. The radial velocity is simply the velocity of the star with respect to our line of sight. The radial velocity will be zero if the star is moving at 90 degrees to our line of sight and will be maximum if it is coming directly towards or away from us.
To obtain the radial velocity we obtain spectroscopic data and utilize the Doppler effect.

(stolen from http://www.gmi.edu/~drussell/Demos/doppler/doppler.html)
We are all familiar with the change in pitch as an ambulance passes us by. As the ambulance moves towards us the sound waves are bunched up and are spaced closer together. This corresponds to a shorter frequency. The sound waves behind the moving source are further apart and have longer frequency. The same principal applies to a source emitting light. As the source moves towards us, the light waves have shorter frequencies than they would if the source was moving away from us.
The frequency of light, F, is related to the wavelength of light, L, in the following way: F = c/L, where c is the speed of light. A higher frequency is the same as a shorter wavelength and vice versa.
We can calculate the speed at which the source is moving by measuring the wavelength of light emitted from it and using the Doppler equation:
(L-Lo)/Lo = v/c.
By taking spectra of stars and measuring the wavelength of a spectral line we can measure the velocity at which the star is moving.
Let us suppose that we've gone to an optical telescope and taken spectra of a star. We plot our spectra and get the following figure:
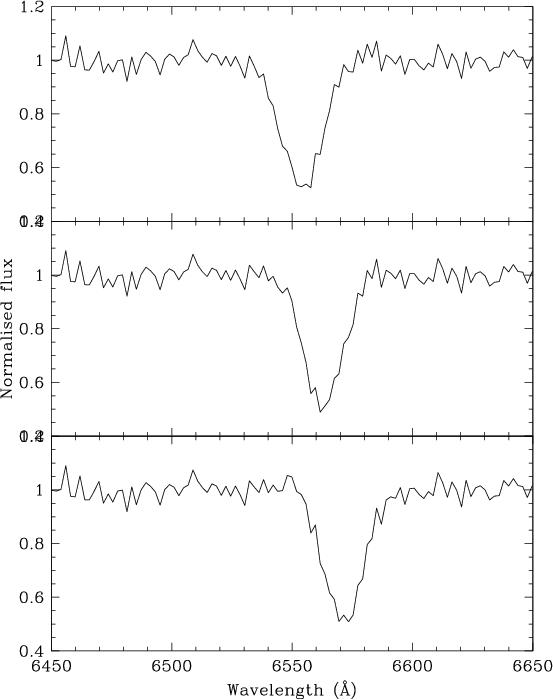
The absorption line is H-alpha which has a rest wavelength of 6562.8 angstroms.
Exercise: From this figure, and using the wavelength form of the Doppler equation above, calculate the velocity of the star taking the minimum of the H-alpha line as a reference point.