solve_for_polynomial_coefficients

halotools.halo_occupation.solve_for_polynomial_coefficients(abcissa, ordinates)

Solves for coefficients of the unique, minimum-degree polynomial that passes through the input abcissa and attains values equal the input ordinates.

Parameters:

abcissa : array

Elements are the abcissa at which the desired values of the polynomial have been tabulated.

ordinates : array

Elements are the desired values of the polynomial when evaluated at the abcissa.

Returns:

polynomial_coefficients : array

Elements are the coefficients determining the polynomial. Element i of polynomial_coefficients gives the degree i coefficient.

Notes

Input arrays abcissa and ordinates can in principle be of any dimension Ndim, and there will be Ndim output coefficients.

The input ordinates specify the desired values of the polynomial when evaluated at the Ndim inputs specified by the input abcissa. There exists a unique, order Ndim polynomial that returns the input ordinates when the polynomial is evaluated at the input abcissa. The coefficients of that unique polynomial are the output of the function.

This function is used by many of the methods in this module. For example, suppose that a model in which the quenched fraction is 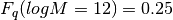and 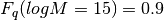. Then this function takes [12, 15] as the input abcissa, [0.25, 0.9] as the input ordinates, and returns the array . The unique polynomial linear in that passes through the input ordinates and abcissa is given by .